بحث عن نظرية فيثاغورس
بحث عن نظرية فيثاغورس سنتعرف عليه بالتفصيل من خلال مقالنا وسنتحدث عن متي يتم استخدام نظرية فيثاغورس والقصة وراء نظرية فيثاغورس.
محتويات الموضوع
بحث عن نظرية فيثاغورس
العناصر
- مقدمة بحث عن نظرية فيثاغورس
- متى نستخدم نظرية فيثاغورس
- قصة نظرية فيثاغورس
- خاتمة بحث عن نظرية فيثاغورس
مقدمة بحث عن نظرية فيثاغورس

يعد فيثاغورث من العلماء الذين سطع نجمهم في علم الرياضيات كما انه له الفضل في تطوير قوانينها وولد فيثاغورث في جزيرة ساموس في اليونان وكان محبا للتجوال في أنحاء العالم وتسجيل الحكم والعبر التي استفاد منها من خلال أسفاره وقد قام بزيارة مصر والهند وكان محبا لكتابات أرسطو و أفلاطون في الفلسفة وقد تم الخلاف حول نظرية فيثاغورث هل تم وضعها مرة واحدة أم على عدة مراحل كما كان محبا للموسيقى فدرس تحركات الوتر وقياس أبعاده ومستوى ارتخائه أو شده لخروج الأصوات مما ساعد بعد ذلك في إنشاء السلم الموسيقي.
متى نستخدم نظرية فيثاغورس

- العمارة والبناء
بالنظر إلى خطين مستقيمين ، تسمح لك نظرية فيثاغورس ، بحساب طول القطر الذي يربطهما ، ويستخدم هذا التطبيق بشكل متكرر في الهندسة المعمارية ، أو النجارة ، أو مشاريع البناء المادية الأخرى ، على سبيل المثال ، لنفترض أنك تقوم ببناء سقف مائل.
وإذا كنت تعرف ارتفاع السقف ، والطول المطلوب تغطيته ، ويمكنك استخدام نظرية فيثاغورس للعثور على الطول القطري لمنحدر السقف ، ويمكنك استخدام هذه المعلومات لقطع العوارض ، ذات الحجم المناسب لدعم السقف ، أو حساب مساحة السقف التي قد تحتاج إليها. - وضع زوايا مربعة
تستخدم نظرية فيثاغورث أيضًا في البناء ، للتأكد من أن المباني مربعة ، والمثلث الذي تتوافق أطواله الجانبية مع نظرية فيثاغورس ، مثل مثلث 3 قدم × 4 قدم × 5 قدم ، وسيكون دائمًا مثلثًا صحيحًا ، وعند وضع الأساس ، أو بناء زاوية مربعة بين جدارين ، سيضع عمال البناء مثلثًا من ثلاثة خيوط تتوافق مع هذه الأطوال ، وإذا تم قياس أطوال السلسلة بشكل صحيح ، فإن الزاوية المقابلة لوتر المثلث ستكون زاوية قائمة ، لذلك سيعرف البنائيون أنهم يقومون ببناء جدرانهم ، أو أسسهم على الخطوط الصحيحة. - بناء الزوايا الصحيحة
الطريقة الأكثر وضوحا لاستخدام نظرية فيثاغورس ، هي بناء الزوايا الصحيحة ، ربما تم وضع قواعد الأهرامات المصرية بهذه الطريقة ، فقد كان معروفًا في ذلك الوقت أن المثلث ذو الجوانب 3 و 4 و 5 له زاوية قائمة ، بالمعنى الدقيق للكلمة ، يستخدم هذا معكوس نظرية فيثاغورس ، ولكن عندما تحدد ثلاثة جوانب مثلثًا فريدًا ، فإنهما متكافئان.
وتساعد نظرية فيثاغورس أيضًا في إيجاد صيغة مفيدة ، لحل المثلثات الأكثر عمومية ، فمن الواضح أن حل المثلثات مهم للمسح ، هذا هو المكان الذي تأتي منه كلمة (علم المثلثات) ، تقسيم المنطقة إلى مثلثات للعثور على مسافة يصعب قياسها مباشرة.
إذا قسمت المثلث إلى قسمين عن طريق رسم عمودي ، من قمة واحدة إلى الجانب المقابل ، فيمكنك تطبيق نظرية فيثاغورس في كل مثلث للعثور على صيغة (قاعدة جيب التمام) ، وللعثور على زاوية معينة من ثلاثة جوانب ، أو الجانب المقابل ل زاوية معروفة نظرا للجانبين الآخرين.
وإذا لم تكن قد رأيت ذلك ، فسيكون من الجيد بالنسبة لك محاولة اكتشافه بنفسك ، فليس الأمر صعبًا ، يجب عليك فقط إدخال مسافتين إضافيتين: دع h يكون ارتفاع المثلث ، و d مسافة العمودية من الزاوية المعروفة ، والقضاء h و d من بعض المعادلات. - التنقل
نظرية فيثاغورس مفيدة للملاحة ثنائية الأبعاد ، حيث يمكنك استخدامه وطولان للعثور على أقصر مسافة ، وعلى سبيل المثال ، إذا كنت في البحر وتتنقل إلى نقطة تبعد 300 ميل شمالًا ، و 400 ميل غربًا ، يمكنك استخدام النظرية للعثور على المسافة من سفينتك ، إلى تلك النقطة وحساب عدد الدرجات إلى الغرب من الشمال ، والتي بحاجة لمتابعة لمتابعة هذه النقطة.
وستكون المسافات بين الشمال ، والغرب ساقي المثلث ، وأقصر خط يربطهما سيكون قطريًا ، ويمكن استخدام نفس المبادئ للملاحة الجوية ، وعلى سبيل المثال ، يمكن للطائرة استخدام ارتفاعها فوق سطح الأرض ، وبُعدها عن مطار الوجهة للعثور على المكان الصحيح ، لبدء النزول إلى ذلك المطار. - المسح
المسح هو العملية التي يقوم بها رسامي الخرائط ، بحساب المسافات ، والارتفاعات الرقمية بين النقاط المختلفة قبل إنشاء الخريطة ، ونظرًا لأن التضاريس غالبًا ما تكون غير متساوية ، يجب على المساحين إيجاد طرق ، لأخذ - قياسات المسافة بطريقة منهجية.
وتُستخدم نظرية فيثاغورس لحساب انحدار منحدرات التلال أو الجبال ، وينظر المساح عبر التلسكوب باتجاه عصا القياس ، على مسافة ثابتة ، بحيث يشكل خط رؤية التلسكوب ، وعصا القياس زاوية قائمة ، بما أن المساح يعرف كلاً من ارتفاع عصا القياس ، والمسافة الأفقية للعصا من التلسكوب ، فيمكنه بعد ذلك استخدام النظرية للعثور على طول المنحدر ، الذي يغطي تلك المسافة ، ومن هذا الطول ، تحديد مدى انحداره.
قصة نظرية فيثاغورس
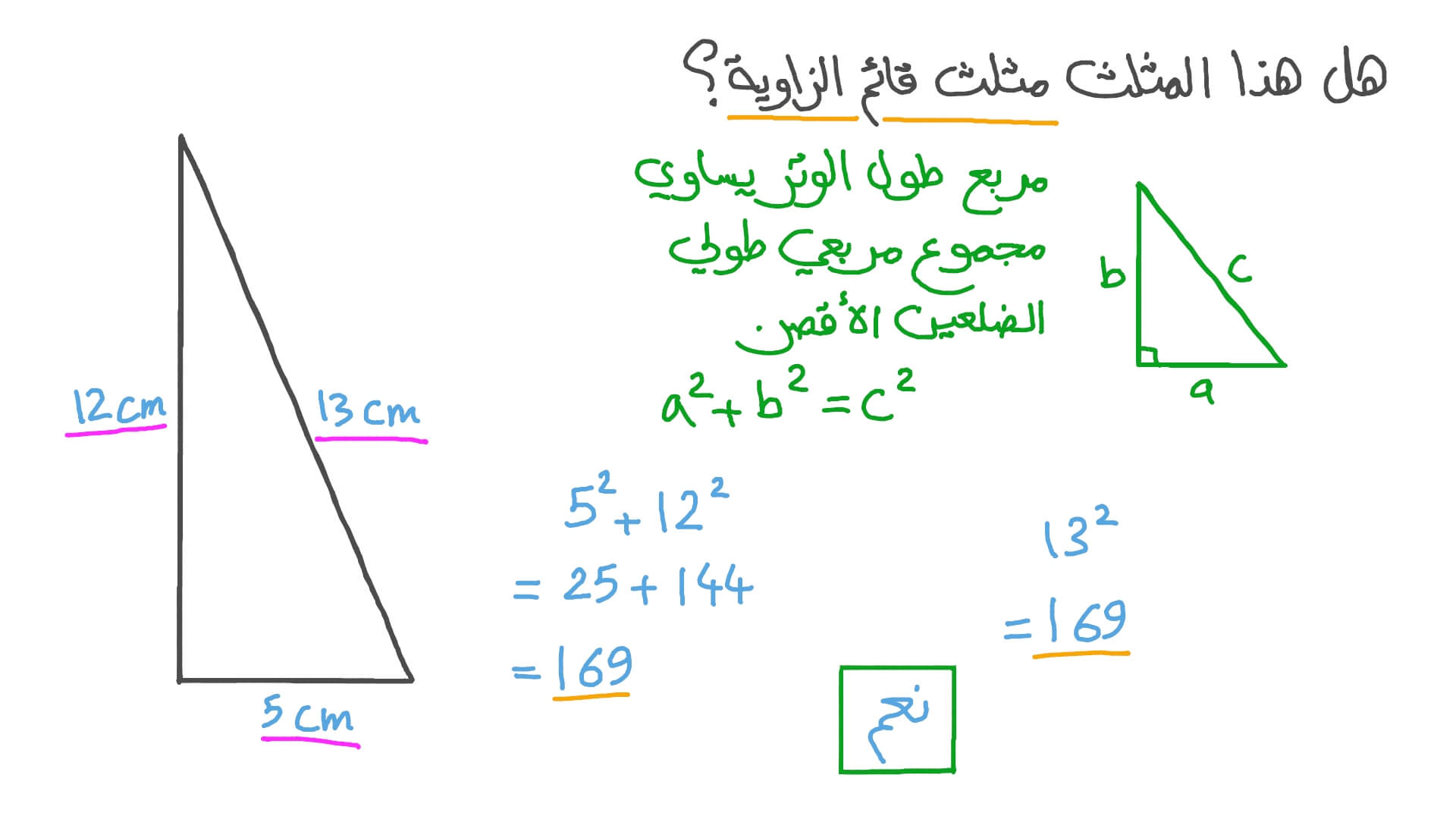
نظرية فيثاغورس هي النظرية الخاصة التى تبحث عن العلاقة بين الهندسة الخاصة بـ المثلث قائم الزاوية و نظرية إقليدس. وتشير نظرية فيثاغورس إلى أن طول الوتر في الجهة المقابلة للزاوية القائمة يساوي المجموع الكلى لمربعين الجانبين الآخرين على أن تكون المعادلة الرياضية على الشكل التالي فلو قمنا بالافتراض أن أطراف المثلث هي أ ب ج وج تمثل طول الوتر الخاص بالمثلث وأطوال الأضلاع الأخرى هي أ وب فتكون المعادلة كالتالي ج 2 = أ 2 + ب 2.
بدأت نظرية فيثاغورس بشكل نظرية موجودة ذات شكل مطول حتى جاء فيثاغورس وقام بإثبات نظريته وصحتها من خلال التجارب والبراهين حيث قام بتجربة عملية وهي إحضار مربعين كبيرين من حيث الحجم وحجمهم مختلف وقام بوضع 4 مثلثات بالقرب من المربعين الكبيرين وعند التطبيق العملي كانت النتيجة أن تطابق المثلثات مع وجود فرق واحد فقط وهو اختلاف ترتيب المثلثات.
خاتمة بحث عن نظرية فيثاغورس

كان للأرقام أهمية ومعاني كبيرة لدى علماء العصور الماضية مقارنةً بعلماء الوقت الحالي، حتى أن العالم فيثاغورس كان يرى أن كل شيء في الكون حوله عبارة عن أرقام، وقد عُدت فيثاغورس النظرية الأشهر في العالم قبل آلاف السنين.
ظهرت نظرية فيثاغورس في بادئ الأمر بشكل معقد للغاية، حتى أتى العالم فيثاغورس وتمكن من إثبات صحتها بطريقة مُبسطة سهلت استخدامها في مجالات عديدة، ومنذ هذا الوقت نُسبت إليه.






